Ашыкча нерсе. Концепциянын мааниси

2024 Автор: Henry Conors | [email protected]. Акыркы өзгөртүү: 2024-02-12 10:19

Макала илим катары статистиканын ролун сүрөттөйт. Куртоз түшүнүгү жана анын илимде колдонулушу каралат.

Статистика. Негизги түшүнүк

Статистика – математика илиминин негизги туундусу. Бул предмет окуучуларда дүйнө таанымдын картинасын калыптандырууга жана окуяларга компетенттүү талдоо жүргүзүүгө багытталган бир катар социалдык дисциплиналарга кирет.

Статистика адамдардын жашоосундагы ар кандай процесстерди жана окуяларды изилдеп, алардын үлгүлөрүн бөлүп көрсөтөт жана баарын кыска статистикалык отчеттор түрүндө көрсөтөт. Мындай илим коомдук пайдалуу жана дайыма жакшыртууну талап кылат. Ашыкча - бул эмне? Бул кемчиликсиз эсептөөнүн тууралыгын аныктоого жардам берген графикалык статистикадагы негизги түшүнүк. Куртоз катуу четтөө болбошу керек.

Статистика адамдардын белгилүү бир кубулуш, окуя жана башкалар жөнүндө ишенимдүү маалыматка болгон муктаждыгын канааттандырууга мүмкүндүк берет. Жашоо факторлорунун динамикасын аныктоо, алардын төмөндөшү, токтоп калуусу же өсүшү - дал ушул илим жасайт.

Азыркы дүйнөдө статистика илимий аренада негизги орундардын бирин ээлейт. Келгиле, "куртоз" түшүнүгүн карап көрөлү. Статистикалык максат жана байкоо деген эмне? Бул түшүнүктөр кайда колдонулат? Мунун баары жөнүндө кененирээк бөлүмдөн окуңузмакала.

Статистикадагы куртоз деген эмне?

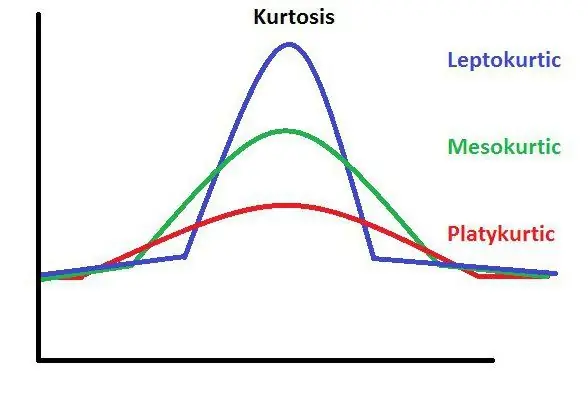
Куртоз – бул бөлүштүрүү графигиндеги ар бир чокунун курчтугун билдирген статистикалык түшүнүк. Аны так эсептөө үчүн атайын формула бар.

Күтүү статистикалык маалыматтардын бир калыпта бөлүштүрүлүшү үчүн куртозис оң санга барабар болушу керек деп айтылат. Сөзмө-сөз айтканда, бул түшүнүк нормадан белгилүү бир четтөө жана статистикалык системанын андан ары анормалдуу өнүгүшүн же иштешин билдирет.

Статистикалык графикте куртоздун ашыкча көрсөтүлүшү туура эмес изилдөөнү же графиктин баштапкы маалыматтарындагы каталарды көрсөтүшү мүмкүн. Мындай түшүнүк скаляр мүнөзгө ээ, демек, акыркы эсептөөдө өзгөрмөлөр же көмөкчү функциялар камтылбаган сан келип чыгышы керек. Куртос ушундай көрүнөт.

Симметриялуу жана асимметриялык бөлүштүрүү деген эмне

Симметриялык типтин таралышы менен байланышкан куртоз нөлгө барабар. Муну график менен ачык көрсөтсө болот. Асимметриялык график нөл эмес санды көрсөтөт. Куртоз ушундайча белгиленет.

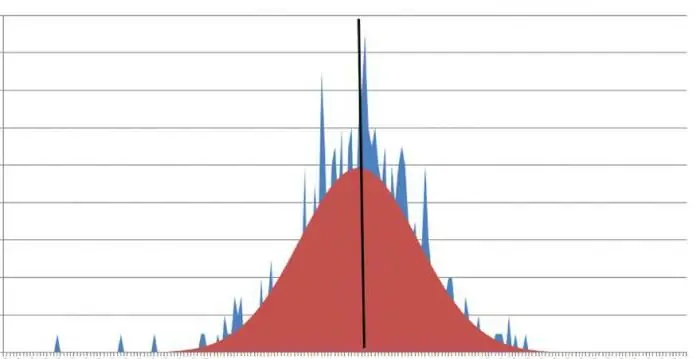
Чонун курчтугу кандай? Курч чокулары бар график куртозис мааниси нөлдөн азыраак сан экенин көрсөтүп турат. Көбүнчө берилген түшүнүк өзүнчө маани менен туюндурулбай калган жагдайлар болот. Бул учурда, ал минус же плюс чексиздикке жакындайт.